Football is so enjoyable to consume because of all the interconnected parts of the game. Deception is of the utmost importance, as it is rare that one team is universally better than its opponent. The small-sample nature of the game, along with the trailing impacts of a single play, places a premium on being diverse — a premium on keeping one's opponent on its toes constantly.
At PFF, we measure things. And if predictability and versatility are important, it follows that being able to measure such a thing is important, too. To do so, we’re going to lean on the godfather of information theory, Claude Shannon. Specifically, we’re going to use a measure called Shannon entropy.
Given a set of probabilities, Shannon entropy is the sum of each of the probabilities multiplied by their logarithm (base 2), all multiplied by -1. For example, for a Bernoulli random variable with probability p = ½ (“success” and “failure” with equal probability), the Shannon entropy is -1/2log(½) -1/2log(½) = log(2) = 1.
This corresponds to the idea that one bit of information is transmitted each time one of these events happens. (We learn something!) If p = 0, the probability of a success is 0 (after one dusts off some calculus) and we get a Shannon entropy of 0 — i.e., No new information is transmitted; we knew a failure was going to occur before it happened, hence nothing learned!
If you jumped over the math, don’t worry: Generally speaking, the more uniform the probabilities are (i.e., less predictable), the higher the Shannon entropy. The more concentrated the probabilities are for one or a few events (i.e., more predictable), the lower the Shannon entropy:
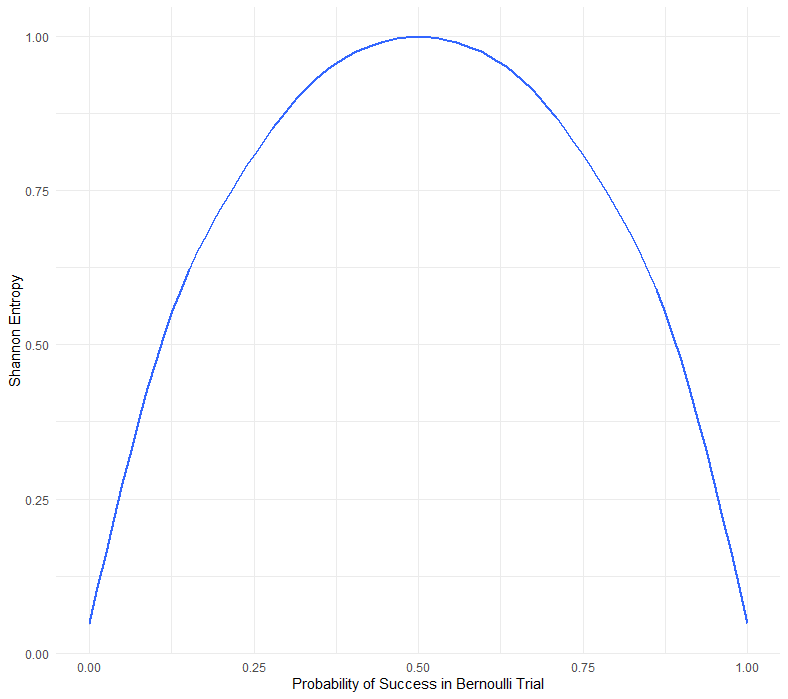
This gives us a tool for measuring how predictable an offensive team is in terms of their run concepts used, a defense is with respect to their coverages, or players are in their usages, for example. ESPN's Mina Kimes mentioned on the PFF Forecast a couple of weeks ago that the versatility of star players like Jamal Adams and Tyrann Mathieu could explain why those teams get more out of their defenses than the sum of the parts would suggest.
DOMINATE FANTASY FOOTBALL & BETTING WITH AI-POWERED DATA & TOOLS TRUSTED BY ALL 32
Unlimited Fantasy League Sync
Fantasy Start/Sit Line-Up Optimizer & Waiver Wire
WR-CB & OL-DL Matchups, PFF Player Grades, & Premium Stats 2.0 Tools
Nathan Jahnkes Rankings - #1 Most Accurate Last 70 Weeks
PFF Best Bets, Player Props, & Power Ranking Tools
NFL Mock Draft Sim with Trades & Draft Grades
Already have a subscription? Log In
© 2024 PFF - all rights reserved.